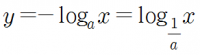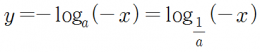| 함수의 종류(3-4글자/한국어) | ||||
|---|---|---|---|---|
| 함수 | 선형함수 | 양함수 | 음함수 (≒음복함수) |
기함수 (≒홀함수) |
| 초함수 | 삼각함수 (≒원함수) |
멱함수 | 실함수 | 여함수 |
| 역함수 | 변함수 | 구함수 | 정함수 | 범함수 |
| 우함수 (≒짝함수) |
도함수 (≒유도함수) |
주기함수 | 지수함수 | 일차함수 (≒선형함수) |
| 편도함수 | 단엽함수 | 단조함수 | 복소함수 | 감소함수 |
| 다엽함수 | 증가함수 | 선출함수 | 오목함수 | 합성함수 |
| 분포함수 | 집합함수 | 다가함수 | 로그함수 대수함수(전 용어) |
영향함수 |
| 직교함수 | 볼록함수 철함수(전 용어) |
일가함수 | 유리함수 (≒유리형함수) |
이차함수 |
| 그린함수 | 분수함수 | 초등함수 | 이가함수 | 동차함수 |
| 정칙함수 | 여할함수 | 특징함수 (≒정의함수,특성함수) |
아벨함수 | 사인함수 |
| 대수함수 | 원시함수 | 무리함수 | 상수함수 정수치함수(전 용어) |
명제함수 |
| 타원함수 | 특수함수 (≒고등함수) |
가법함수 | 연속함수 | 다원함수 |
| 해석함수 | 유계함수 | 고유함수 | 초월함수 | 조화함수 |
| 계단함수 | 목적함수 | 대칭함수 | 델타함수 | 정현함수 |
| ||||||||||||
개요[편집]
| 사전 | ● |
교육과정 연계[편집]
고2 수학 I에 등장한다. (2015년 교육과정 기준)
기본형[편집]
- 로그함수의 기본형은 다음과 같다.
로그함수의 이동[편집]
※모든 조건은 a>0, a≠1 입니다.
평행이동[편집]
x축 평행이동[편집]
- 로그함수 y=logax를 x축 방향으로 m만큼 평행이동했을 때 식은 다음과 같다.
y축 평행이동[편집]
- 로그함수 y=logax를 y축 방향으로 n만큼 평행이동했을 때 식은 다음과 같다.
x축, y축 평행이동[편집]
- 로그함수 y=logax를 x축 방향으로 m만큼, y축 방향으로 n만큼 평행이동했을 때 식은 다음과 같다.
대칭이동[편집]
x축에 대해 대칭이동[편집]
- 로그함수 y=logax를 x축에 대해 대칭이동했을 때 식은 다음과 같다.
y축에 대해 대칭이동[편집]
- 로그함수 y=logax를 y축에 대해 대칭이동했을 때 식은 다음과 같다.
원점에 대해 대칭이동[편집]
- 로그함수 y=logax를 원점에 대해 대칭이동했을 때 식은 다음과 같다.
로그함수의 역함수[편집]
지수함수의 역함수를 구하는 방법은 다음과 같다. 예를 든 함수는 y=log2x 이다.
정의역과 치역 구하기[편집]
- 역함수 문서에 설명해 놨지만, 역함수의 정의에 의하여 정의역과 치역이 서로 바뀐다. 고로, 정의역과 치역을 바꿔야 한다.
y=log2x의 정의역 : {x|x≥0인 실수}, 치역 : {y|y는 모든 실수}
변수의 위치 바꾸기[편집]
- 그 다음, 정의역과 치역을 바꿔야 하므로 변수의 위치를 바꾼다.
x=log2y
로그의 정의 이용하기[편집]
- y에 대해 식을 쓰기 위해, 로그의 정의를 이용하여 식을 변형한다. (logaN = x일 때, ax = N)
y=2x
범위 정하기[편집]
- 역함수는 원래 함수의 치역이 정의역이므로, 범위를 반드시 써 줘야 한다. (로그함수의 정의역은 모든 실수이므로, 굳이 범위를 써 줄 필요가 없다.)
y=2x
로그함수와 지수함수의 관계[편집]
위의 역함수를 구하는 방법으로 알 수 있는 사실이 있다.
- 로그함수 y=logax (a>0, a≠1)와 지수함수 y=ax (a>0, a≠1)는 서로 역함수 관계이다.
로그함수의 그래프[편집]
두 함수의 차이점[편집]
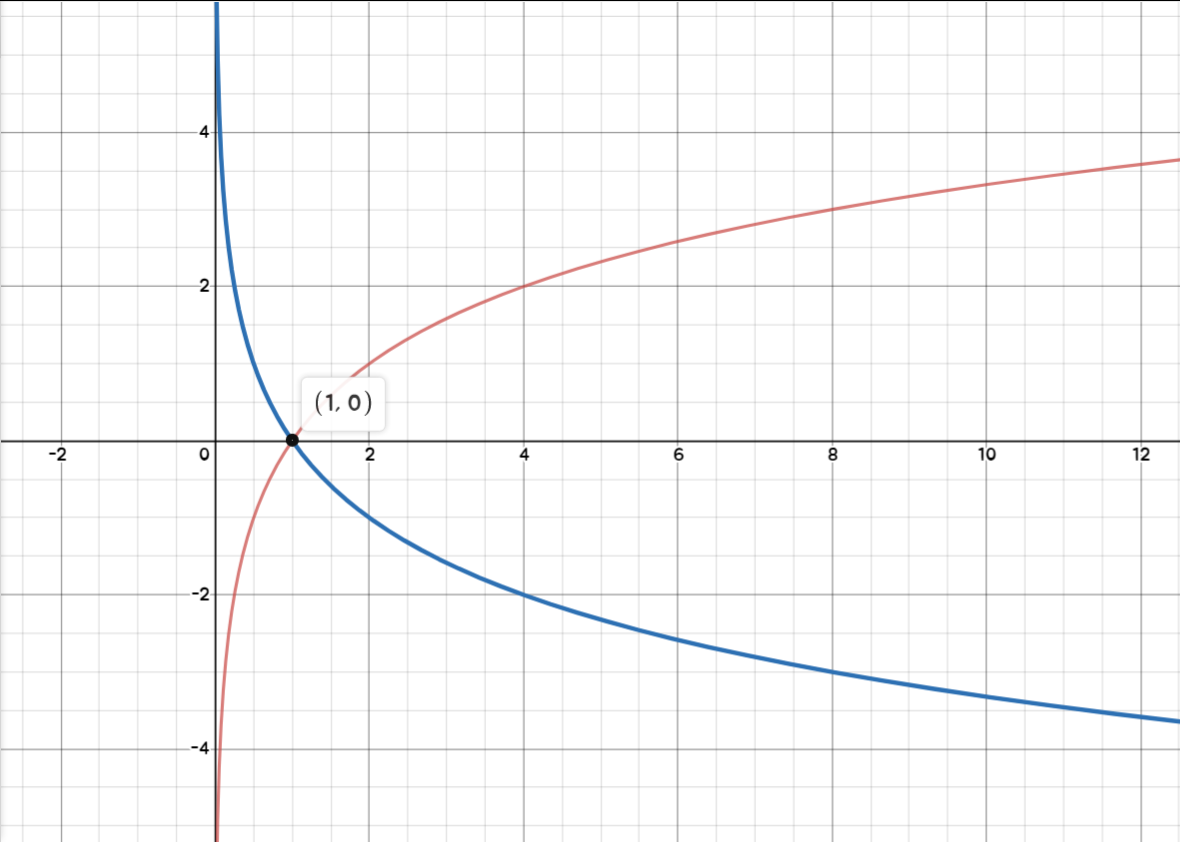
빨간색은 y=logax(a>1), 파란색은 y=logax(0<a<1) 이다.
- 두 함수의 차이점
| 두 로그함수의 공통점/차이점 | |||
|---|---|---|---|
| 그래프의 식 | y=logax (a>1) | y=logax (0<a<1) | |
| 지나는 점 | (1,0) | (1,0) | |
| 그래프의 증감 | 증가함수 | 감소함수 | |
| 점근선 | x=0(y축) | x=0(y축) | |
로그함수의 도함수[편집]
도함수 문서를 참고하면 로그함수의 미분법을 알 수 있다.